Create your experimental design with Python command

Introduction
Design of Experiment (DOE) is an important activity for any scientist, engineer, or statistician planning to conduct experimental analysis. This exercise has become critical in this age of rapidly expanding field of data science and associated statistical modeling and machine learning. A well-planned DOE can give a researcher meaningful data set to act upon with optimal number of experiments preserving critical resources.
After all, aim of Data Science is essentially to conduct highest quality scientific investigation and modeling with real world data. And to do good science with data, one needs to collect it through carefully thought-out experiment to cover all corner cases and reduce any possible bias.
What is a scientific experiment?
In its simplest form, a scientific experiment aims at predicting the outcome by introducing a change of the preconditions, which is represented by one or more independent variables, also referred to as “input variables” or “predictor variables.” The change in one or more independent variables is generally hypothesized to result in a change in one or more dependent variables, also referred to as “output variables” or “response variables.” The experimental design may also identify control variables that must be held constant to prevent external factors from affecting the results.
What is Experimental Design?
Experimental design involves not only the selection of suitable independent, dependent, and control variables, but planning the delivery of the experiment under statistically optimal conditions given the constraints of available resources. There are multiple approaches for determining the set of design points (unique combinations of the settings of the independent variables) to be used in the experiment.
Main concerns in experimental design include the establishment of validity, reliability, and replicability. For example, these concerns can be partially addressed by carefully choosing the independent variable, reducing the risk of measurement error, and ensuring that the documentation of the method is sufficiently detailed. Related concerns include achieving appropriate levels of statistical power and sensitivity.
Need for careful design of experiment arises in all fields of serious scientific, technological, and even social science investigation — computer science, physics, geology, political science, electrical engineering, psychology, business marketing analysis, financial analytics, etc…
Options for open-source DOE builder package in Python?
Unfortunately, majority of the state-of-the-art DOE generators are part of commercial statistical software packages like JMP (SAS) or Minitab.
However, a researcher will surely be benefited if there exists an open-source code which presents an intuitive user interface for generating an experimental design plan from a simple list of input variables.
There are a couple of DOE builder Python packages but individually they don’t cover all the necessary DOE methods and they lack a simplified user API, where one can just input a CSV file of input variables’ range and get back the DOE matrix in another CSV file.
I am glad to announce the availability of a Python-based DOE package (with permissive MIT license) for anybody to use and enhance. You can download the code base from my GitHub Repo, here.
Features
This set of codes is a collection of functions which wrap around the core packages (mentioned below) and generate design-of-experiment (DOE) matrices for a statistician or engineer from an arbitrary range of input variables.
Limitation of the foundation packages used
Both the core packages, which act as foundations to this repo, are not complete in the sense that they do not cover all the necessary functions to generate DOE table that a design engineer may need while planning an experiment. Also, they offer only low-level APIs in the sense that the standard output from them are normalized numpy arrays. It was felt that users, who may not be comfortable in dealing with Python objects directly, should be able to take advantage of their functionalities through a simplified user interface.
Simplified user interface
User just needs to provide a simple CSV file with a single table of variables and their ranges (2-level i.e. min/max or 3-level). Some of the functions work with 2-level min/max range while some others need 3-level ranges from the user (low-mid-high). Intelligence is built into the code to handle the case if the range input is not appropriate and to generate levels by simple linear interpolation from the given input. The code will generate the DOE as per user’s choice and write the matrix in a CSV file on to the disk. In this way, the only API user is exposed to are input and output CSV files. These files then can be used in any engineering simulator, software, process-control module, or fed into process equipment.
Design options
Following design options are available to generate from input variables,
- Full factorial,
- 2-level fractional factorial,
- Plackett-Burman,
- Sukharev grid,
- Box-Behnken,
- Box-Wilson (Central-composite) with center-faced option,
- Box-Wilson (Central-composite) with center-inscribed option,
- Box-Wilson (Central-composite) with center-circumscribed option,
- Latin hypercube (simple),
- Latin hypercube (space-filling),
- Random k-means cluster,
- Maximin reconstruction,
- Halton sequence based,
- Uniform random matrix
How to use it?
What supporting packages are required?
First make sure you have all the necessary packages installed. You can simply run the .bash (Unix/Linux) and .bat (Windows) files provided in the repo, to install those packages from your command line interface. They contain the following commands,
pip install numpy
pip install pandas
pip install matplotlib
pip install pydoe
pip install diversipy
Errata for using PyDOE
Please note that as installed, PyDOE will throw some error related to type conversion. There are two options
- I have modified the pyDOE code suitably and included a file with re-written functions in the repo. This is the file called by the program while executing, so you should see no error.
- If you encounter any error, you could try to modify the PyDOE code by going to the folder where pyDOE files are copied and copying the two files
doe_factorial.pyanddoe_box_behnken.pysupplied with this repo.
One simple command to generate a DOE
Note this is just a code repository and not a installer package. For the time being, please clone this repo from GitHub, store all the files in a local directory and start using the software by simply typing,
**python Main.py**
After this, a simple menu will be printed on the screen and you will be prompted for a choice of number (a DOE) and name of the input CSV file (containing the names and ranges of your variables). You must have an input parameters CSV file stored in the same directory that you are running this code from. Couple of example CSV files are provided in the repo. Feel free to modify them as per your needs. You should use the supplied generic CSV file as an example. Please put the factors in the columns and the levels in the row (not the other way around). Example of the sample parameters range is as follows,

Is an installer/Python library available?
At this time, No. I plan to work on turning this into a full-fledged Python library which can be installed from PyPi repository by a PIP command. But I cannot promise any timeline for that :-) If somebody wants to collaborate and work on an installer, please feel free to do so.
Examples
Full/fractional factorial designs
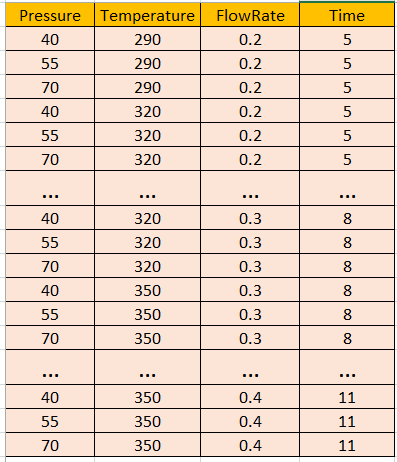
Imagine a generic example of a chemical process in a plant where the input file contains the table for the parameters range as shown above. If we build a full-factorial DOE out of this, we will get a table with 81 entries because 4 factors permuted in 3 levels result in 3⁴=81 combinations!
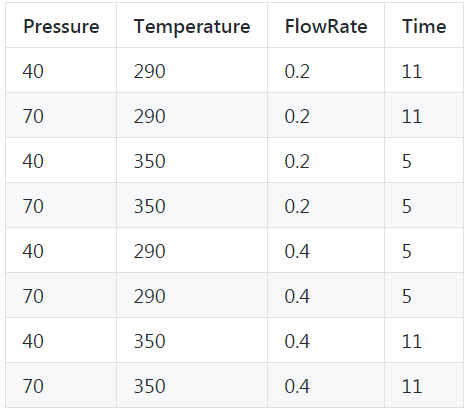
Clearly the full-factorial designs grows quickly! Engineers and scientists therefore often use half-factorial/fractional-factorial designs where they confound one or more factors with other factors and build a reduced DOE. Let’s say we decide to build a 2-level fractional factorial of this set of variables with the 4th variables as the confounding factor (i.e. not an independent variable but as a function of other variables). If the functional relationship is “A - B - C - BC” i.e. the 4th parameter vary depending only on 2nd and 3rd parameter, the output table could look like,
Central-composite design
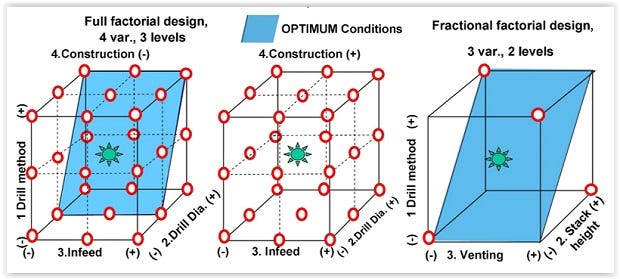
A Box-Wilson Central Composite Design, commonly called ‘a central composite design,’ or response-surface-methodology (RSM) contains an embedded factorial or fractional factorial design with center points that is augmented with a group of ‘star points’ that allow estimation of curvature. The method was introduced by George E. P. Box and K. B. Wilson in 1951. The main idea of RSM is to use a sequence of designed experiments to obtain an optimal response.

Central composite designs are of three types. One central composite design consists of cube points at the corners of a unit cube that is the product of the intervals [-1,1], star points along the axes at or outside the cube, and center points at the origin. This is called Circumscribed (CCC) designs.
Inscribed (CCI) designs are as described above, but scaled so the star points take the values -1 and +1, and the cube points lie in the interior of the cube.
Faced (CCF) designs have the star points on the faces of the cube. Faced designs have three levels per factor, in contrast with the other types that have five levels per factor. The following figure shows these three types of designs for three factors.
Read this wonderful tutorial for more information about this kind of design philosophy.
Latin Hypercube design
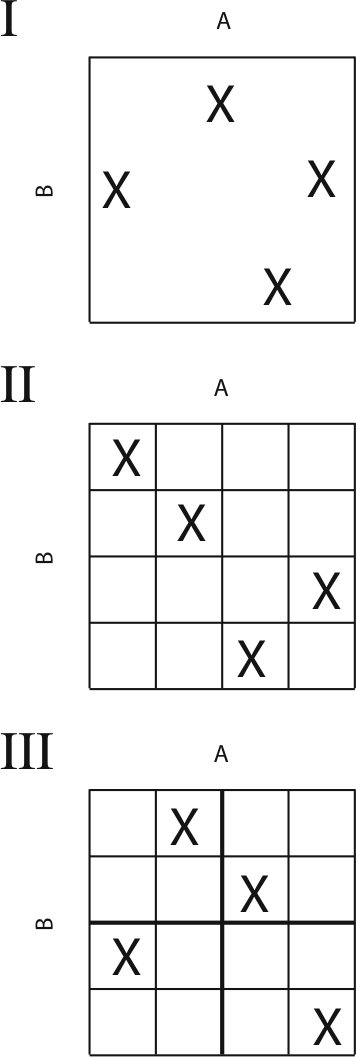
Sometimes, a set of randomized design points within a given range could be attractive for the experimenter to asses the impact of the process variables on the output. Monte Carlo simulations are close example of this approach. However, a Latin Hypercube design is better choice for experimental design rather than building a complete random matrix as it tries to subdivide the sample space in smaller cells and choose only one element out of each sub-cell.
In statistical sampling, a square grid containing sample positions is a Latin square if (and only if) there is only one sample in each row and each column. A Latin Hypercube is the generalization of this concept to an arbitrary number of dimensions, whereby each sample is the only one in each axis-aligned hyperplane containing it. When sampling a function of N variables, the range of each variable is divided into M equally probable intervals. M sample points are then placed to satisfy the Latin Hypercube requirements; this forces the number of divisions, M, to be equal for each variable. This sampling scheme does not require more samples for more dimensions (variables); this independence is one of the main advantages of this sampling scheme. This way, a more ‘uniform spreading’ of the random sample points can be obtained.
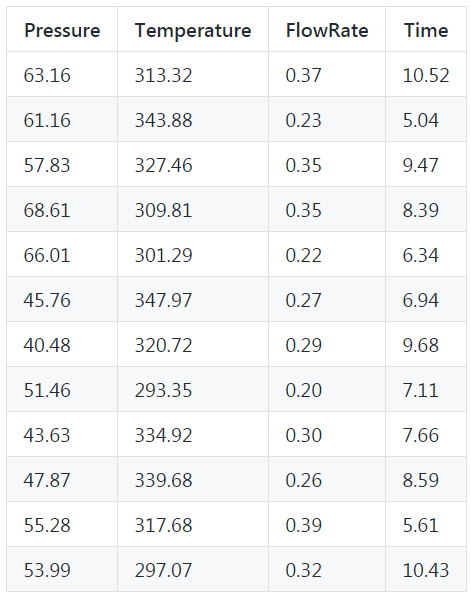
User can choose the density of sample points. For example, if we choose to generate a Latin Hypercube of 12 experiments from the same input files, that could look like following. Of course, there is no guarantee that you will get the same matrix if you run this function because this are randomly sampled, but you get the idea!
You can read further on this here.
Further extensions
Currently, one can only generate various DOE and save the output in a CSV file. However, some useful extensions can be thought of,
- More advanced randomized sampling based on model information gain i.e. sample those volumes of the hyperplane where more information can be gained for the expected model. This of course requires an idea of the input/output model i.e. which parameters are more important.
- Add-on statistical functions to generate descriptive statistics and basic visualizations from the output from various experiments generated by the DOE function.
- Basic machine learning add-on functions to analyze the output from various experiments and identify the most important parameters.
Ifyou have any questions or ideas to share, please contact the author at tirthajyoti[AT]gmail.com. Also you can check author’s GitHub repositories for other fun code snippets in Python, R, or MATLAB and machine learning resources. If you are, like me, passionate about machine learning/data science, please feel free to add me on LinkedIn or follow me on Twitter.
Suggest:
☞ Python Tutorial for Data Science
☞ Learn Python in 12 Hours | Python Tutorial For Beginners
☞ Complete Python Tutorial for Beginners (2019)
☞ Python Tutorials for Beginners - Learn Python Online
☞ Python Programming Tutorial | Full Python Course for Beginners 2019