Hypothesis testing in Machine learning using Python

Well probably all who are beginner in machine learning or in intermediate level or statistic student heard about this buzz word hypothesis testing.
Today i will give a brief introduction over this topic which created headache for me when i was learning this. I put all those concept together and examples using python.
some question in mind before i will go for broader things -
What is hypothesis testing ? why do we use it ? what are basic of hypothesis ? which are important parameter of hypothesis testing ?
Let’s start one by one :
1. What is hypothesis testing ?
Hypothesis testing is a statistical method that is used in making statistical decisions using experimental data. Hypothesis Testing is basically an assumption that we make about the population parameter.
Ex : you say avg student in class is 40 or a boy is taller than girls.
all those example we assume need some statistic way to prove those. we need some mathematical conclusion what ever we are assuming is true.
2. why do we use it ?
Hypothesis testing is an essential procedure in statistics. A hypothesis test evaluates two mutually exclusive statements about a population to determine which statement is best supported by the sample data. When we say that a finding is statistically significant, it’s thanks to a hypothesis test.
3. what are basic of hypothesis ?

The basic of hypothesis is normalisation and standard normalisation. all our hypothesis is revolve around basic of these 2 terms. let’s see these.

You must be wondering what’s difference between these two image, one might say i don’t find, while other will see some flatter graph compare to steep. well buddy this is not what i want to represent , in 1st first you can see there are different normal curve all those normal curve can have different mean’s and variances where as in 2nd image if you notice the graph is properly distributed and mean =0 and variance =1 always. concept of z-score comes in picture when we use standardised normal data.
Normal Distribution -
A variable is said to be normally distributed or have a normal distribution if its distribution has the shape of a normal curve — a special bell-shaped curve. … The graph of a normal distribution is called the normal curve, which has all of the following properties: 1. The mean, median, and mode are equal.

Standardised Normal Distribution —
A standard normal distribution is a normal distribution with mean 0 and standard deviation 1

Which are important parameter of hypothesis testing ?
Null hypothesis :- In inferential statistics, the null hypothesis is a general statement or default position that there is no relationship between two measured phenomena, or no association among groups
In other words it is a basic assumption or made based on domain or problem knowledge.
Example : a company production is = 50 unit/per day etc.
Alternative hypothesis :-
The alternativehypothesis is the hypothesis used in hypothesis testing that is contrary to the null hypothesis. It is usually taken to be that the observations are the result of a real effect (with some amount of chance variation superposed)
Example : a company production is !=50 unit/per day etc.

Level of significance: Refers to the degree of significance in which we accept or reject the null-hypothesis. 100% accuracy is not possible for accepting or rejecting a hypothesis, so we therefore select a level of significance that is usually 5%.
This is normally denoted with alpha(maths symbol ) and generally it is 0.05 or 5% , which means your output should be 95% confident to give similar kind of result in each sample.
Type I error: When we reject the null hypothesis, although that hypothesis was true. Type I error is denoted by alpha. In hypothesis testing, the normal curve that shows the critical region is called the alpha region
Type II errors: When we accept the null hypothesis but it is false. Type II errors are denoted by beta. In Hypothesis testing, the normal curve that shows the acceptance region is called the beta region.
One tailed test :- A test of a statistical hypothesis , where the region of rejection is on only one side of the sampling distribution , is called a one-tailed test.
Example :- a college has ≥ 4000 student or data science ≤ 80% org adopted.
Two-tailed test :- A two-tailed test is a statistical test in which the critical area of a distribution is two-sided and testswhether a sample is greater than or less than a certain range of values. If the sample being testedfalls into either of the critical areas, the alternative hypothesis is accepted instead of the null hypothesis.
Example : a college != 4000 student or data science != 80% org adopted

P-value :- The P value, or calculated probability, is the probability of finding the observed, or more extreme, results when the null hypothesis (H 0) of a study question is true — the definition of ‘extreme’ depends on how the hypothesis is being tested.
If your P value is less than the chosen significance level then you reject the null hypothesis i.e. accept that your sample gives reasonable evidence to support the alternative hypothesis. It does NOT imply a “meaningful” or “important” difference; that is for you to decide when considering the real-world relevance of your result.
Example : you have a coin and you don’t know whether that is fair or tricky so let’s decide null and alternate hypothesis
H0 : a coin is a fair coin.
H1 : a coin is a tricky coin. and alpha = 5% or 0.05
Now let’s toss the coin and calculate p- value ( probability value).
Toss a coin 1st time and result is tail- P-value = 50% (as head and tail have equal probability)
Toss a coin 2nd time and result is tail, now p-value = 50/2 = 25%
and similarly we Toss 6 consecutive time and got result as P-value = 1.5% but we set our significance level as 95% means 5% error rate we allow and here we see we are beyond that level i.e. our null- hypothesis does not hold good so we need to reject and propose that this coin is a tricky coin which is actually.
Degree of freedom :- Now imagine you’re not into hats. You’re into data analysis.You have a data set with 10 values. If you’re not estimating anything, each value can take on any number, right? Each value is completely free to vary.But suppose you want to test the population mean with a sample of 10 values, using a 1-sample t test. You now have a constraint — the estimation of the mean. What is that constraint, exactly? By definition of the mean, the following relationship must hold: The sum of all values in the data must equal n x mean, where n is the number of values in the data set.
So if a data set has 10 values, the sum of the 10 values must equal the mean x 10. If the mean of the 10 values is 3.5 (you could pick any number), this constraint requires that the sum of the 10 values must equal 10 x 3.5 = 35.
With that constraint, the first value in the data set is free to vary. Whatever value it is, it’s still possible for the sum of all 10 numbers to have a value of 35. The second value is also free to vary, because whatever value you choose, it still allows for the possibility that the sum of all the values is 35.
Now Let’s see some of widely used hypothesis testing type :-
- T Test ( Student T test)
- Z Test
- ANOVA Test
- Chi-Square Test
T- Test :- A t-test is a type of inferential statistic which is used to determine if there is a significant difference between the means of two groups which may be related in certain features. It is mostly used when the data sets, like the set of data recorded as outcome from flipping a coin a 100 times, would follow a normal distribution and may have unknown variances. T test is used as a hypothesis testing tool, which allows testing of an assumption applicable to a population.
T-test has 2 types : 1. one sampled t-test 2. two-sampled t-test.
One sample t-test : The One Sample t Test determines whether the sample mean is statistically different from a known or hypothesised population mean. The One Sample t Test is a parametric test.
Example :- you have 10 ages and you are checking whether avg age is 30 or not. (check code below for that using python)
from scipy.stats import ttest_1samp
import numpy as np
ages = np.genfromtxt(“ages.csv”)
print(ages)
ages_mean = np.mean(ages)
print(ages_mean)
tset, pval = ttest_1samp(ages, 30)
print(“p-values”,pval)
if pval < 0.05: # alpha value is 0.05 or 5%
print(" we are rejecting null hypothesis")
else:
print("we are accepting null hypothesis")
Output for above code is :

**Two sampled T-test :-**The Independent Samples t Test or 2-sample t-test compares the means of two independent groups in order to determine whether there is statistical evidence that the associated population means are significantly different. The Independent Samples t Test is a parametric test. This test is also known as: Independent t Test.
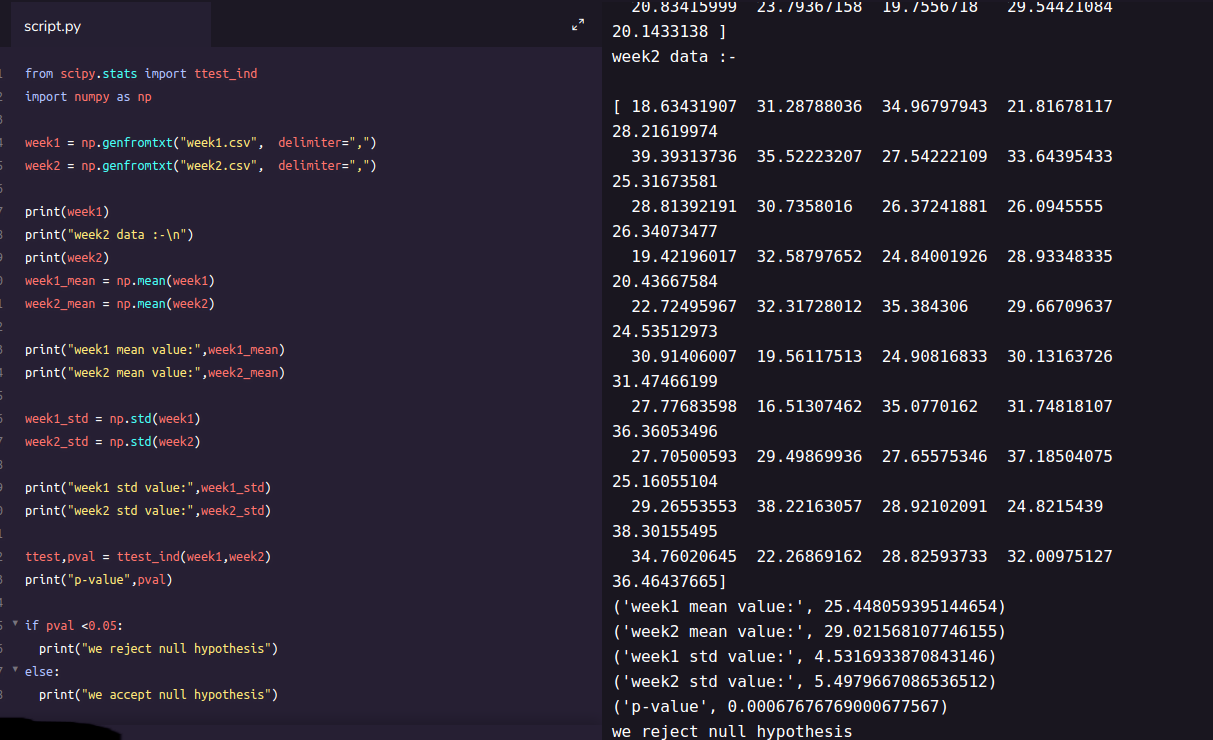
Example : is there any association between week1 and week2 ( code is given below in python)
from scipy.stats import ttest_ind
import numpy as np
week1 = np.genfromtxt("week1.csv", delimiter=",")
week2 = np.genfromtxt("week2.csv", delimiter=",")
print(week1)
print("week2 data :-\n")
print(week2)
week1_mean = np.mean(week1)
week2_mean = np.mean(week2)
print("week1 mean value:",week1_mean)
print("week2 mean value:",week2_mean)
week1_std = np.std(week1)
week2_std = np.std(week2)
print("week1 std value:",week1_std)
print("week2 std value:",week2_std)
ttest,pval = ttest_ind(week1,week2)
print("p-value",pval)
if pval <0.05:
print("we reject null hypothesis")
else:
print("we accept null hypothesis")
Paired sampled t-test :- The paired sample t-test is also called dependent sample t-test. It’s an uni variate test that tests for a significant difference between 2 related variables. An example of this is if you where to collect the blood pressure for an individual before and after some treatment, condition, or time point.
H0 :- means difference between two sample is 0
H1:- mean difference between two sample is not 0
check the code below for same
import pandas as pd
from scipy import stats
df = pd.read_csv("blood_pressure.csv")
df[['bp_before','bp_after']].describe()
ttest,pval = stats.ttest_rel(df['bp_before'], df['bp_after'])
print(pval)
if pval<0.05:
print("reject null hypothesis")
else:
print("accept null hypothesis")
When you can run a Z Test.
Several different types of tests are used in statistics (i.e. f test, chi square test, t test). You would use a Z test if:
- Your sample size is greater than 30. Otherwise, use a t test.
- Data points should be independent from each other. In other words, one data point isn’t related or doesn’t affect another data point.
- Your data should be normally distributed. However, for large sample sizes (over 30) this doesn’t always matter.
- Your data should be randomly selected from a population, where each item has an equal chance of being selected.
- Sample sizes should be equal if at all possible.
Example again we are using z-test for blood pressure with some mean like 156 (python code is below for same) one-sample Z test.
import pandas as pd
from scipy import stats
from statsmodels.stats import weightstats as stests
ztest ,pval = stests.ztest(df['bp_before'], x2=None, value=156)
print(float(pval))
if pval<0.05:
print("reject null hypothesis")
else:
print("accept null hypothesis")
Two-sample Z test- In two sample z-test , similar to t-test here we are checking two independent data groups and deciding whether sample mean of two group is equal or not.
H0 : mean of two group is 0
H1 : mean of two group is not 0
Example : we are checking in blood data after blood and before blood data.(code in python below)
ztest ,pval1 = stests.ztest(df['bp_before'], x2=df['bp_after'], value=0,alternative='two-sided')
print(float(pval1))
if pval<0.05:
print("reject null hypothesis")
else:
print("accept null hypothesis")
ANOVA (F-TEST) :- The t-test works well when dealing with two groups, but sometimes we want to compare more than two groups at the same time. For example, if we wanted to test whether voter age differs based on some categorical variable like race, we have to compare the means of each level or group the variable. We could carry out a separate t-test for each pair of groups, but when you conduct many tests you increase the chances of false positives. The analysis of variance or ANOVA is a statistical inference test that lets you compare multiple groups at the same time.
F = Between group variability / Within group variability
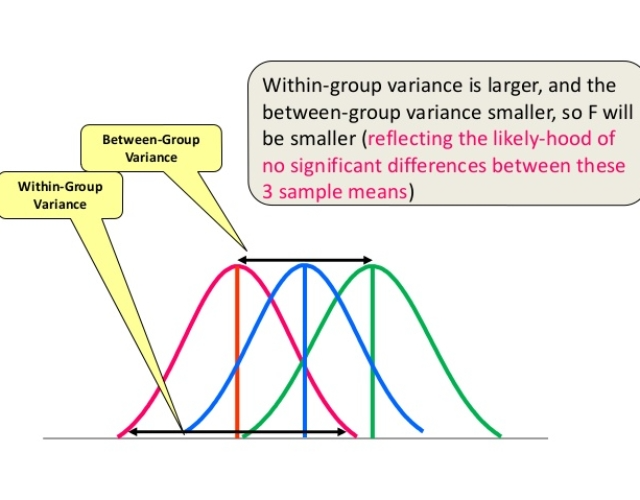
Unlike the z and t-distributions, the F-distribution does not have any negative values because between and within-group variability are always positive due to squaring each deviation.
One Way F-test(Anova) :- It tell whether two or more groups are similar or not based on their mean similarity and f-score.
Example : there are 3 different category of plant and their weight and need to check whether all 3 group are similar or not (code in python below)
df_anova = pd.read_csv('PlantGrowth.csv')
df_anova = df_anova[['weight','group']]
grps = pd.unique(df_anova.group.values)
d_data = {grp:df_anova['weight'][df_anova.group == grp] for grp in grps}
F, p = stats.f_oneway(d_data['ctrl'], d_data['trt1'], d_data['trt2'])
print("p-value for significance is: ", p)
if p<0.05:
print("reject null hypothesis")
else:
print("accept null hypothesis")
Two Way F-test :- Two way F-test is extension of 1-way f-test, it is used when we have 2 independent variable and 2+ groups. 2-way F-test does not tell which variable is dominant. if we need to check individual significance then Post-hoc testing need to be performed.
Now let’s take a look at the Grand mean crop yield (the mean crop yield not by any sub-group), as well the mean crop yield by each factor, as well as by the factors grouped together
import statsmodels.api as sm
from statsmodels.formula.api import ols
df_anova2 = pd.read_csv("https://raw.githubusercontent.com/Opensourcefordatascience/Data-sets/master/crop_yield.csv")
model = ols('Yield ~ C(Fert)*C(Water)', df_anova2).fit()
print(f"Overall model F({model.df_model: .0f},{model.df_resid: .0f}) = {model.fvalue: .3f}, p = {model.f_pvalue: .4f}")
res = sm.stats.anova_lm(model, typ= 2)
res
Chi-Square Test- The test is applied when you have two categorical variables from a single population. It is used to determine whether there is a significant association between the two variables.
For example, in an election survey, voters might be classified by gender (male or female) and voting preference (Democrat, Republican, or Independent). We could use a chi-square test for independence to determine whether gender is related to voting preference
check example in python below
df_chi = pd.read_csv('chi-test.csv')
contingency_table=pd.crosstab(df_chi["Gender"],df_chi["Shopping?"])
print('contingency_table :-\n',contingency_table)
#Observed Values
Observed_Values = contingency_table.values
print("Observed Values :-\n",Observed_Values)
b=stats.chi2_contingency(contingency_table)
Expected_Values = b[3]
print("Expected Values :-\n",Expected_Values)
no_of_rows=len(contingency_table.iloc[0:2,0])
no_of_columns=len(contingency_table.iloc[0,0:2])
ddof=(no_of_rows-1)*(no_of_columns-1)
print("Degree of Freedom:-",ddof)
alpha = 0.05
from scipy.stats import chi2
chi_square=sum([(o-e)**2./e for o,e in zip(Observed_Values,Expected_Values)])
chi_square_statistic=chi_square[0]+chi_square[1]
print("chi-square statistic:-",chi_square_statistic)
critical_value=chi2.ppf(q=1-alpha,df=ddof)
print('critical_value:',critical_value)
#p-value
p_value=1-chi2.cdf(x=chi_square_statistic,df=ddof)
print('p-value:',p_value)
print('Significance level: ',alpha)
print('Degree of Freedom: ',ddof)
print('chi-square statistic:',chi_square_statistic)
print('critical_value:',critical_value)
print('p-value:',p_value)
if chi_square_statistic>=critical_value:
print("Reject H0,There is a relationship between 2 categorical variables")
else:
print("Retain H0,There is no relationship between 2 categorical variables")
if p_value<=alpha:
print("Reject H0,There is a relationship between 2 categorical variables")
else:
print("Retain H0,There is no relationship between 2 categorical variables")
You can get all code in my git repository.
ah, finally we came to end of this article. I hope this article would have helped. any feedback is always appreciated.
Recommended Reading
☞ WebScraping With Python, Beautiful Soup, and Urllib3
☞ How to optimize your Jupyter Notebook
☞ How to Build an E-commerce Website with Django and Python
☞ Seaborn Heatmap Tutorial (Python Data Visualization)
☞ Is your Django app slow? Think like a data scientist, not an engineer
Suggest:
☞ Machine Learning Zero to Hero - Learn Machine Learning from scratch
☞ Complete Python Tutorial for Beginners (2019)
☞ Python Tutorials for Beginners - Learn Python Online
☞ What is Python and Why You Must Learn It in [2019]
☞ Learn Python in 12 Hours | Python Tutorial For Beginners
☞ Python Programming Tutorial | Full Python Course for Beginners 2019